Hi,大家好,美好的一天从这里开始,今天主要讲解平面度怎么测量,这个方法既简单又实用,以及关于平面,误差,测量等等各种相关干货,想要做好首先一定要把基本功练好了,否者是很难持续提升的。
平面度的测量与评定方法概述
平面度误差是指实际被测平面与理想平面的距离。平面度误差的测量方法和直线度误差的测量方法类似。包括间隙法、指示器法、光轴法、干涉法、液面法、水平仪法、自准直仪法和坐标测量法。与直线度误差测量方法类似,平面度测量方法按照其测量原理可分为相同的三种方法。只有第三种方法需要对测得数据进行分析,才能获得平面度误差。根据处理测量数据方法的不同,又可分为两类。一类是测量点的测量结果不需要经过累积计算或坐标转换等处理,测量点测量结果可看作是相互独立的,如坐标测量机法、光轴法、钢丝法。另一类测量点直接测量的结果需要经过累积计算或坐标转换等处理如水平仪法、自准直仪法等。其单点测量不确定度的确定方法也和直线度误差相同。
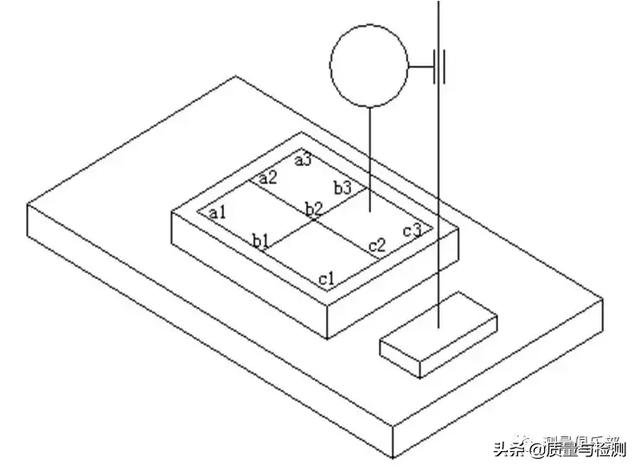
平面度的评定方法包括最小包容区域法、最小二乘平面法、对角线平面法和三远点平面法。
1.最小区域法
最小区域法是指用相互平行的两个平面包容实际被测平面,这两个平面的距离的最小值即为最小区域法评定出的平面度误差。这两平面遵循的原则是这两平行平面和被测平面至少有四个接触点。这四个点需满足交又准则或三角形准则。最小区域法评定出的误差值最小,作为最后仲裁依据。
2.最小二乘平面法
用最小二乘法评定平面度误差时,评定的基准平面是最小二乘平面SLS,最小二乘平面确定是利用各测量点到平面的距离的平方和为最小值。取得各点相对于该平面的偏离值中的最大偏离值和最小偏离值之差作为平面度误差值。点在平面上方为正,在平面下方为负。
3.对角线法和三远点法
对角线法的基准平面是包含实际表面的一条对角线的两个对角点,并且和另一条对角线平行的平面SDL。
三远点法的基准平面是包含实际平面上距离较远的三个点的平面STP,平面STP的方程可由三点的坐标直接求得。
评定基准平面SDL、STP求得以后,再取得各点相对于该平面的偏离值中的最大偏离值和最小偏离值之差作为平面度误差值。点在平面上方为正,在平面下方为负。
综上可知,最小二乘平面法计算方便简洁,下面以最小二乘平面法为例介绍平面度的评定过程。
平面度的最小二乘模型
如下图所示,在直角坐标系中得到平面上n个点的坐标值。
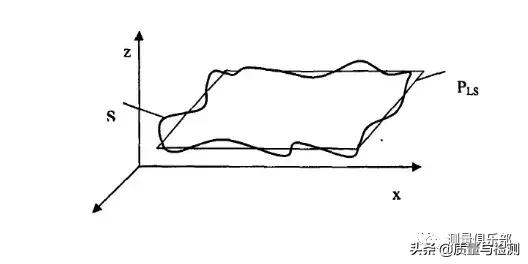
假定测得点坐标为(x,y,z,),最小二乘平面为:z=ax+by+c,其中a,b,c为待定参数。根据最小二乘原理得最小二乘平面的待定参数a,b,c为:
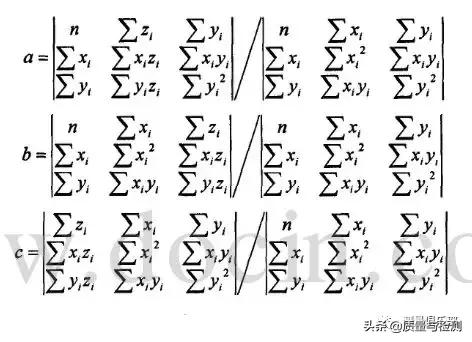
取坐标距离的最大值(XM,YM,ZM)和最小值(XL,YL,ZL),则平面度误差为:
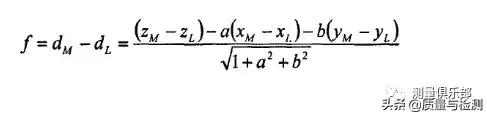
好了,今天我就为大家说到这里,希望能帮到大家,认真看完了这篇平面度怎么测量:最新这个方法既简单又实用文章,感觉收获很多,可以帮忙分享一下。
本文发布者:万事通,不代表寂寞网立场,转载请注明出处:https://www.jimowang.com/p/13007.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 jimowangmail@126.com 举报,一经查实,本站将立刻删除。

